概率机器人第六章习题解答
第六章
1. 早期应用特征识别的机器人使用放置在环境中的易于识别的人工地标导航。安装这种标记的一个好地方就是天花板(为什么?)。一个经典的例子是视觉标记,假定将以下标记附着在天花板上。

令该标记的地球坐标是$x_m$和$y_m$,其相对于全局坐标系统的方向为$\theta_m$。用$x_r$、$y_r$和$\theta_r$来表示机器人的位姿。
现在假定给定一个例程,可以检测立体相机的图像平面中的标记。令$x_i$和$y_i$表示图像平面中标记的坐标,$\theta_i$表示其角度方向。相机焦距为f。由投影几何学知道,$x-y$空间的每一个位移$d$都将一个比例位移$d\frac{f}{h}$投射到图像平面。(必须在你的坐标系统中做一些选择,使这些选择清晰)。问题如下:
(a)当图像坐标是$(x_i,y_i,\theta_i)$,机器人在$(x_r,y_r,\theta_r)$时,数学推导期望标记的位置[全局坐标$(x_m,y_m,\theta_m)$]。
(b)给出一个由机器人位姿$(x_r,y_r,\theta_r)$和标记坐标$(x_m,y_m,\theta_m)$,计算图像坐标$(x_i,y_i,\theta_i)$的数学公式。
(c)现在假定已知实际的标记坐标$(x_m,y_m,\theta_m)$和图像坐标$(x_i,y_i,\theta_i)$,给出确定机器人坐标$(x_r,y_r,\theta_r)$的数学公式。
(d)到目前为止都是假定仅有一个标记。现在假设有多个上述这种(不可分辨的)标记。机器人必须能看到多少个这样的标记才能唯一地确定其位姿?给出这样的配置,并论证为什么这样就足够了。
提示:回答这个问题时不必考虑测量的不确定性。同时,注意标记是对称的,这对问题的答案会有影响。
安装这种标记的位置是天花板是因为:
1.遮挡标记的障碍物较少。
2.因为1990s的研究多为在平面运动的轮式机器人,因此只需要测量其$x-y$平面上的位姿即可。
本题的示意图如图所示:
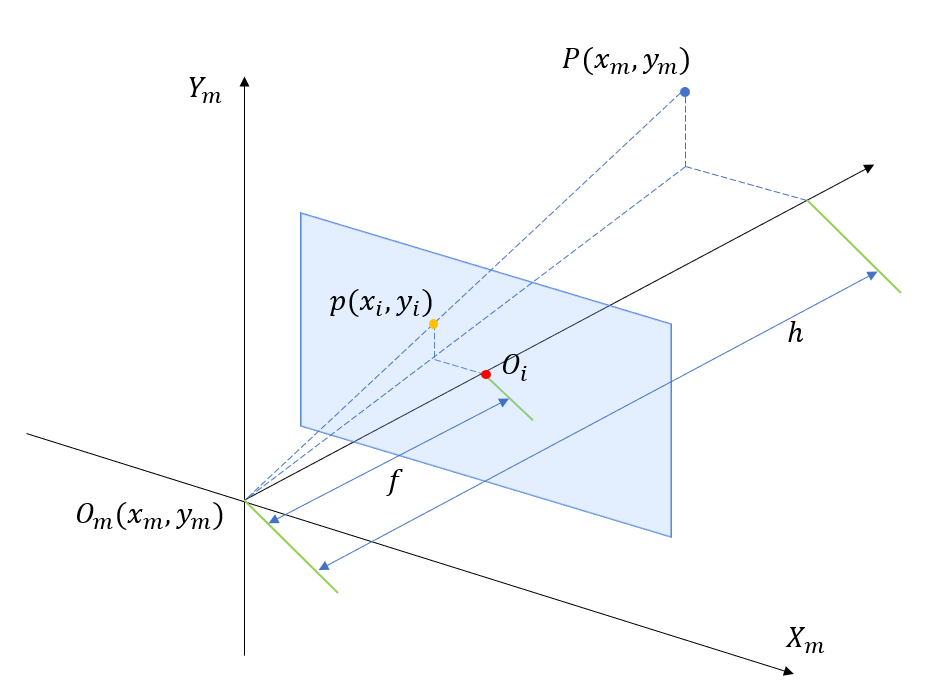
(a)假设从机器人上表面到屋顶的垂直距离为$h$。先理解图像坐标的含义,其$x、y、\theta$都是相对于机器人坐标系的坐标,不需要进行坐标变换。但是需要注意的是,$\theta_i$应该是图像的方向,而非标记的方向,否则第二道题没法做(没东西可以泰勒展开)。但是问题在于,如果$\theta_i$是图像的方向,那么标记的方向就没有办法得知,也就是说,$\theta_m$是一个没有用的数据。只能假设图像的方向即为标记相对于机器人的方向,否则标记的方向只能为$arctan(\frac{y_m}{x_m})$。
可以直接求得,相对于机器人而言,标记的坐标为:
$$ P' = (\frac{h}{f}x_i,\frac{h}{f}y_i,\theta_i) $$
在此基础上,将机器人坐标系变换到世界坐标系,可得:
$$ P = \begin{pmatrix}\frac{h}{f}\sqrt{x_i^2+y_i^2}cos(\theta_i+\theta_r-arctan(\frac{y_i}{x_i}))+x_r \\ \frac{h}{f}\sqrt{x_i^2+y_i^2}sin(\theta_i+\theta_r-arctan(\frac{y_i}{x_i}))+y_r \\ \theta_i+\theta_r \end{pmatrix}$$
(b)若图像与机器人坐标系重合,即$\theta_i = 0$,可得:
$$ p' = (\frac{f}{h}(x_m-x_r),\frac{f}{h}(y_m-y_r)) $$
现在将图像坐标系旋转$\theta_m - \theta_r$,可得:
$$ p = \begin{pmatrix}
\sqrt{x_p^2+y_p^2} cos(\theta_m-\theta_r-arctan(\frac{y_p}{x_p}))\\
\sqrt{x_p^2+y_p^2} sin(\theta_m-\theta_r-arctan(\frac{y_p}{x_p}))\\
\theta_m-\theta_r
\end{pmatrix} $$
其中,$$ x_p = \frac{f}{h}(x_m-x_r), y_p = \frac{f}{h}(y_m-y_r) $$
(c)由(a)很容易得到:
$$ O_m = \begin{pmatrix}
x_m - \frac{h}{f}\sqrt{x_i^2+y_i^2}cos(\theta_i+\theta_r-arctan(\frac{y_i}{x_i}))\\
y_m - \frac{h}{f}\sqrt{x_i^2+y_i^2}sin(\theta_i+\theta_r-arctan(\frac{y_i}{x_i}))\\
\theta_m-\theta_i
\end{pmatrix} $$
(d)因为标记是对称的,所以当看到一个标记时,应该有4种可能的角度。可以分几种情况讨论这个问题。
-
机器人可以分辨多个标记之间的空间关系。
这种情况下,仅仅需要两个标记即可唯一地确定机器人的位姿。这里提供一个可能的方案。

可以把上述两个标记看成一个图形,这个图形是有方向的,因此可以唯一地确定机器人的位姿。
-
机器人不能分辨多个标记之间的空间关系,只能逐个识别。
这种情况下,无论多少个标记都不能唯一地确定机器人位姿,因为每次观测是独立的,都有四种可能的角度。
2. 在本习题中,请将上一个习题中的计算扩展到包括误差协方差。为了简化计算,现在假设一个非对称标记,可以估计该标记的绝对方向:

同时,为了简化,假设在方向上没有噪声。但是,图像平面的$x-y$估计是有噪声的。具体来说,令测量服从协方差为
$$ \Sigma = \begin{pmatrix}
\sigma^2 & 0 & 0\\
0 & \sigma^2 & 0\\
0 & 0 & 0\\
\end{pmatrix} $$
均值为0的高斯噪声。(其中$\sigma^2$为正值)计算上述三个问题的相关协方差。问题如下:
(a)给定图像坐标$(x_i,y_i,\theta_i)$和机器人位姿$(x_r,y_r,\theta_r)$,则$(x_m,y_m,\theta_m)$值的误差协方差是多少?
(b)给定机器人位姿$(x_r,y_r,\theta_r)$和标记坐标$(x_m,y_m,\theta_m)$,则$(x_i,y_i,\theta_i)$值的误差协方差是多少?
(c)给定标记坐标$(x_m,y_m,\theta_m)$和图像坐标$(x_i,y_i,\theta_i)$,则机器人位姿$(x_r,y_r,\theta_r)$值的误差协方差是多少?
注意,不是所有的分布都是高斯的。对于本习题,最好是采用泰勒级数展开去获得一个高斯后验,但是你必须解释是怎样做的。
(a)以$x_m$为例。
$$ \begin{aligned}
x_m &= \frac{h}{f}\sqrt{x_i^2+y_i^2}cos(\theta_i+\theta_r-arctan(\frac{y_i}{x_i}))+x_r \\
&\overset{Taylor}{===} \frac{h}{f}\sqrt{x_i^2+y_i^2} (1-\frac{(\theta_i+\theta_r-arctan(\frac{y_i}{x_i}))^2}{2})\\
保留噪声&\rightarrow\frac{h}{f}\sqrt{x_i^2+y_i^2}(\frac{arctan^2(\frac{y_i}{x_i})}{2})\\
&\overset{Taylor}{===} \frac{h}{f}\frac{y_i^2}{2 x_i^2}\sqrt{x_i^2+y_i^2}\\
\Sigma_x &= (\frac{h^2}{2f^2}\sigma^2,\frac{h^2}{2f^2}\sigma^2,0)\\
同理,\Sigma_y &= (\frac{2h^2}{f^2}\sigma^2,\frac{2h^2}{f^2}\sigma^2,0)
\end{aligned}$$
(b)图像平面方差已经给定,为:
$$ \Sigma = \begin{pmatrix}
\sigma^2 & 0 & 0\\
0 & \sigma^2 & 0\\
0 & 0 & 0\\
\end{pmatrix} $$
(c)观察等式的形式可以发现噪声应该与(a)数值相反。
$$ \Sigma = \begin{pmatrix}
\frac{h^2}{2f^2}\sigma^2 & -\frac{h^2}{2f^2}\sigma^2 & 0\\
-\frac{2h^2}{f^2}\sigma^2 & \frac{2h^2}{f^2}\sigma^2 & 0\\
0 & 0 & 0\\
\end{pmatrix} $$
3.现在请实现sample_marker_model算法的例程,这里将标记位置$(x_m,y_m,\theta_m)$和在图像平面$(x_i,y_i,\theta_i)$感知的标记位置作为输入,产生机器人位姿$(x_r,y_r,\theta_r)$的输出样本。该标记是与习题1相同的不可分辨的标记:

对以下参数(你可以在图上忽略方向$\theta_r$)产生一个机器人坐标$x_r$和$y_r$的样本图。
| 问题编号 | $x_m(cm)$ | $y_m(cm)$ | $\theta_m(^o)$ | $x_i(cm)$ | $y_i(cm)$ | $\theta_i(^o)$ | $h/f$ | $\sigma^2(cm^2)$ |
|---|---|---|---|---|---|---|---|---|
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 200 | 0.1 |
| 2 | 0 | 0 | 0 | 1 | 0 | 0 | 200 | 0.1 |
| 3 | 0 | 0 | 0 | 2 | 0 | 45 | 200 | 0.1 |
| 4 | 0 | 0 | 0 | 3 | 0 | 45 | 200 | 1.0 |
| 5 | 50 | 150 | 10 | 1 | 6 | 200 | 250 | 0.5 |
你的所有图应该显示坐标轴及单位。注意,如果你不能设计一个确切的采样器,提供一个近似的,并解释你的近似。
- 先预处理:
5个问题的位姿分别为:
$$ X_1 = (0,0,0),\Sigma = (2000,8000,0)\\X_2 = (200,0,0)\\X_3 = (565.69,0,0)\\X_4 = (848.53,0,0),\Sigma = (20000,80000,0)\\X_5 = (1016.51,-1124.04,2.97),\Sigma = (15625,62500,0) $$ - 画图
import matplotlib.pyplot as plt
import numpy as np
import random
color = ['c', 'b', 'g', 'r', 'm', 'y', 'k', 'w']
u1 = np.array([0,200,565.69,848.53,1016.51]) # 第一个高斯分布的均值
sigma1 = np.array([2000,2000,2000,20000,15625]) # 第一个高斯分布的方差
u2 = np.array([0,0,0,0,-1124.04]) # 第二个高斯分布的均值
sigma2 = np.array([8000,8000,8000,80000,62500]) # 第二个高斯分布的方差
for i in range(0,5):
x = np.empty(0)
y = np.empty(0)
x_rand = np.random.normal(loc=u1[i],scale=np.sqrt(sigma1[i]),size=(1,1000)).flatten()
y_rand = np.random.normal(loc=u2[i],scale=np.sqrt(sigma2[i]),size=(1,1000)).flatten()
for cnt in range(0,1000):
x = np.append(x,x_rand[cnt])
y = np.append(y,y_rand[cnt])
plt.scatter(x,y,c=color[i],s=1)
plt.xlabel('X(cm)')
plt.ylabel('Y(cm)')
plt.show()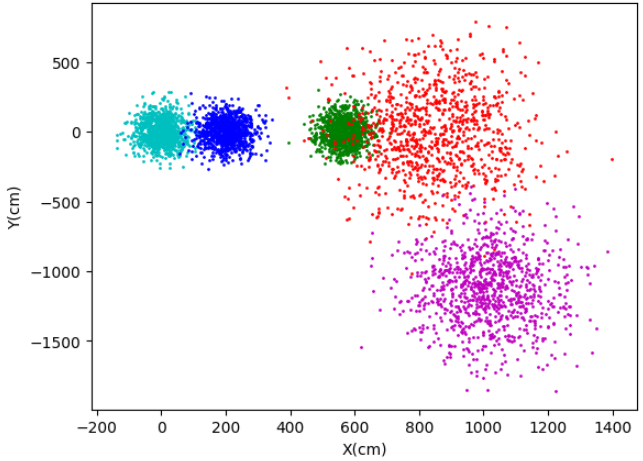
4.本习题中,你需要使用一个具有声呐传感器(经常在室内机器人技术中用到的类型)的机器人。将传感器放在平整墙面的前面,距离为$d$,角度为$\Phi$。测量传感器检测墙的频率。画出不同的$d$值(以0.5m为增量)和不同$\Phi$值(以$5^o$为增量)下的频率,你发现了什么?
传感器测距一次超声波往返的距离为:
$$ L = \frac{2d}{cos\Phi} $$
传感器测距一次的周期为:
$$ T = \frac{L}{v} = \frac{2d}{v \cdot cos\Phi} $$
传感器的频率为:
$$ f = \frac{1}{T} = \frac{v \cdot cos\Phi}{2d} $$
import matplotlib.pyplot as plt
import numpy as np
import random
import math
from mpl_toolkits.mplot3d import Axes3D
v = 340
phi = np.arange(0, 90, 5)
d = np.arange(0.5,10,0.5)
X, Y = np.meshgrid(phi, d)
Z = v*np.cos(X*np.pi/180)/2/Y
fig1 = plt.figure()
ax1 = plt.axes(projection='3d')
ax1.scatter3D(X,Y,Z,alpha=0.3,cmap='winter') #绘制散点图
ax1.contour(X,Y,Z,zdir='x', offset=0,cmap="rainbow") #生成x方向投影,投到y-z平面
ax1.contour(X,Y,Z,zdir='y', offset=0,cmap="rainbow") #生成y方向投影,投到x-z平面
ax1.set_xlabel('Phi')
ax1.set_xlim(0, 90) #拉开坐标轴范围显示投影
ax1.set_ylabel('d')
ax1.set_ylim(0.5, 10)
ax1.set_zlabel('f')
ax1.set_zlim(0, 300)
plt.show()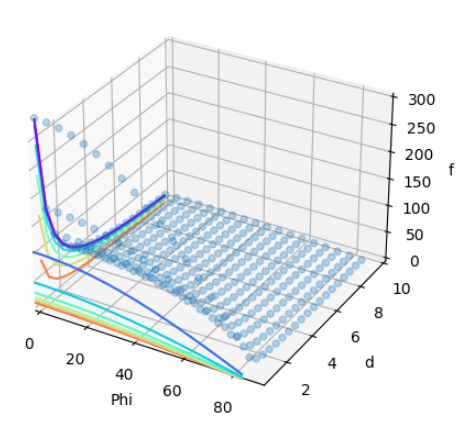
[...]第六章习题解答[...]
《她爱上了我的谎》韩国剧高清在线免费观看:https://www.jgz518.com/xingkong/140876.html
你的文章充满了创意,真是让人惊喜。 https://www.4006400989.com/qyvideo/97886.html
独家揭秘:热血传奇私服攻城申请攻略,称霸沙城一招致胜!:https://501h.com/jinbi/2024-10-16/42781.html
你的文章让我感受到了快乐,每天都要来看一看。 http://www.55baobei.com/Xe3f8HsI1e.html
《恋如雨止~口袋中的愿望~》日本剧高清在线免费观看:https://www.jgz518.com/xingkong/115287.html
《财星高照》海外剧高清在线免费观看:https://www.jgz518.com/xingkong/43312.html
《恋如雨止~口袋中的愿望~》日本剧高清在线免费观看:https://www.jgz518.com/xingkong/115287.html