第二章

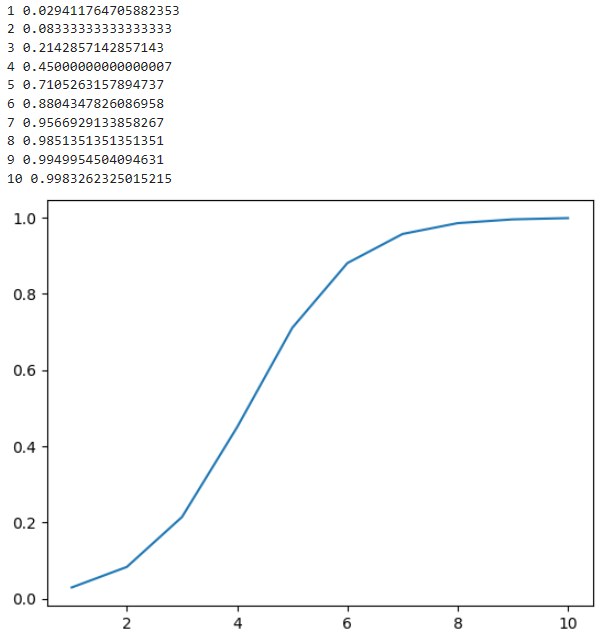
1.机器人使用一个可以测量0-3m距离的传感器。为了简化，假定真实的距离在这个范围中均匀分布。很不幸的是，传感器会坏掉。当传感器故障时，不管传感器的锥形测量范围内实际测距结果应该是多少，其输出测距值均小于1m。已知对于传感器故障的先验概率是p=0.01。设想机器人查询了N次传感器，每次测量值都小于1m。对于N=1，2，···，10的传感器故障的后验概率是多少？用公式表示相关的概率模型。

假定传感器处于两种可能的状态的一种：故障或不故障。用X表示传感器故障情况，Y表示传感器测量结果，先验概率为：

$ p(X_1 = \text{broken}) = 0.01\\
p(X_1 = \text{normal}) = 0.99 $

当传感器故障情况下，测量值小于1m的概率为：

$ p(Y_t = 1m | X_t = \text{broken}) = 1 $

当传感器正常时，测量值小于1m的概率为：

$ p(Y_t = 1m | X_t = \text{normal}) = \frac{1}{3} $

在第一次测量时，N=1，测量值小于1m，由贝叶斯准则可知：

$ \begin{aligned}
p(X_1 = \text{broken} | Y_1 = 1m) &= \eta p(Y_1 = 1m | X_1 = \text{broken})p(X_1 = \text{broken})\\
&= \eta \times 1 \times 0.01\\
&= 0.01 \eta
\end{aligned} $
$ \begin{aligned}
p(X_1 = \text{normal} | Y_1 = 1m) &= \eta p(Y_1 = 1m | X_1 = \text{normal})p(X_1 = \text{normal})\\
&= \eta \times \frac{1}{3} \times 0.99\\
&= 0.33 \eta
\end{aligned} $

第一次测量后，传感器故障与不故障的后验概率和应该为1，即：

$$ p(X_1 = \text{broken} | Y_1 = 1m) + p(X_1 = \text{normal} | Y_1 = 1m) = 1 \\
0.01 \eta + 0.33 \eta = 1 \\
\eta = \frac{1}{0.34} = 2.94 $$

第一次测量的后验作为第二次测量的先验，即：

$ p(X_2 = \text{broken}) = p(X_1 = \text{broken} | Y_1 = 1m) = 0.01 \eta = 0.0294 $
$ p(X_2 = \text{normal}) = p(X_1 = \text{normal} | Y_1 = 1m) = 0.33 \eta = 0.9702 $

之后的测量以此类推。

import matplotlib.pyplot as plt
import numpy as np

ANS = np.empty(0)
I = np.empty(0)

def is_broken(px):
    eta = 1/(px+(1-px)/3)
    px1 = eta*px
    return px1

ans = 0.01

for i in range(1,11):
    ans = is_broken(ans)
    ANS = np.append(ANS,ans)
    I = np.append(I,i)
    print(i,ans)

plt.plot(I,ANS)
plt.show()

程序结果如下图所示：

2.设想住在一个白天天气为晴、多云或者雨的地方。天气转移函数是如下的转移表所示的马尔科夫链：

今天	明天
	晴	多云	雨
晴	0.8	0.2	0
多云	0.4	0.4	0.2
雨	0.2	0.6	0.2

(1)设第一天是晴（Day1 = sunny），接下来第二天是多云、第三天是多云、第四天是雨天（Day2 = cloudy、Day3 = cloudy、Day4 = rainy）的概率是多少？

$ \begin{aligned}
p(Day2=cloudy) = &0.2\\
p(Day3=cloudy) = &0.8 \times 0.2 + 0.2 \times 0.4 + 0 = 0.24\\
p(Day4=rainy) = &0.8 \times 0.8 \times 0 + 0.8 \times 0.2 \times 0.2 + \\
&0.2 \times 0.4 \times 0 + 0.2 \times 0.4 \times 0.2 + 0.2 \times 0.2 \times 0.2 = 0.056
\end{aligned} $

(2)根据这个状态转移函数写出一个能随机产生“天气”序列的仿真器。

(3)使用你的仿真器确定这个马尔可夫链的平稳分布，平稳分布衡量任意一天是晴、多云、雨的概率。

$$
\begin{pmatrix}
{A_{t}}&{B_{t}}&{C_{t}}
\end{pmatrix} \times
\begin{pmatrix}
0.8 & 0.2 & 0\\
0.4 & 0.4 & 0.2\\
0.2 & 0.6 & 0.2
\end{pmatrix} =
\begin{pmatrix}
{0.8A_t+0.4B_t+0.2C_t}\\
{0.2A_t+0.4B_t+0.6C_t}\\
{0A_t+0.2B_t+0.2C_t}
\end{pmatrix}^{T} =
\begin{pmatrix}
{A_{t+1}}&{B_{t+1}}&{C_{t+1}}
\end{pmatrix}
$$
其中A、B、C分别为晴、多云、雨的概率。例如第一天天气是晴，则第一天的状态矩阵为：$ \begin{pmatrix}1&0&0\end{pmatrix} $
计算出的第二天的状态矩阵为：$ \begin{pmatrix}0.8&0.2&0\end{pmatrix} $
随机产生天气的函数可以由随机数产生，在此省略。计算天气序列概率的程序为：

import matplotlib.pyplot as plt
import numpy as np

ans = np.array([1,0,0])
K = np.array([[0.8,0.2,0],[0.4,0.4,0.2],[0.2,0.6,0.2]])
ANS1 = np.empty(0)
ANS2 = np.empty(0)
ANS3 = np.empty(0)
I = np.empty(0)

for i in range(1,50):
    ans = np.dot(ans,K)
    ANS1 = np.append(ANS1,ans[0])
    ANS2 = np.append(ANS2,ans[1])
    ANS3 = np.append(ANS3,ans[2])
    I = np.append(I,i)
    print(i,ans)

plt.plot(I,ANS1)
plt.plot(I,ANS2)
plt.plot(I,ANS3)
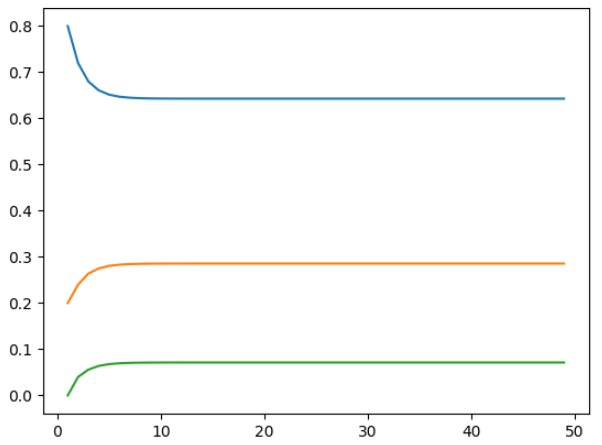
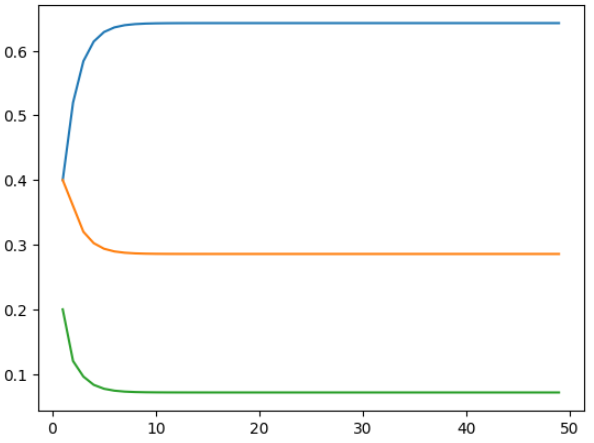
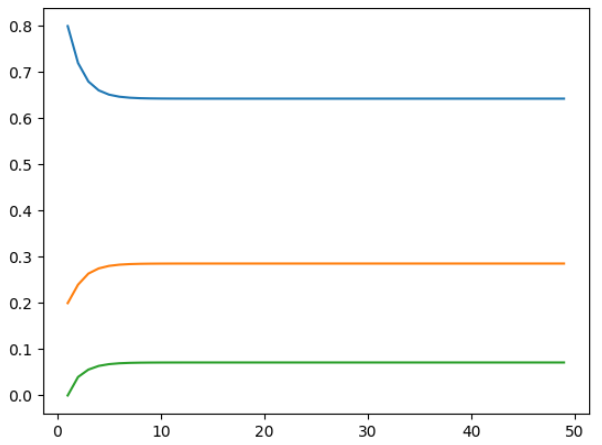
plt.show()

程序中的50即为程序停止的天数。程序输出结果如下图所示。可知迭代到第25天左右概率即趋近于稳定，且最终结果与初始值无关。

(4)你能制定一个闭式方案来根据上面的状态转移矩阵计算平稳分布吗？

即：$ \begin{pmatrix} A & B & C \end{pmatrix} \times K = \begin{pmatrix} A & B & C \end{pmatrix} $
$ \left\{
\begin{matrix}
A \times 0.8 + B \times 0.4 + C \times 0.2 = A \\
A \times 0.2 + B \times 0.4 + C \times 0.6 = B \\
A \times 0 + B \times 0.2 + C \times 0.2 = C \\
A+B+C=1
\end{matrix}
\right.
\rightarrow
\left\{
\begin{matrix}
2B+C-A=0 \\
A-3B+3C=0 \\
B-4C = 0\\
A+B+C=1
\end{matrix}
\right.
\rightarrow
\left\{
\begin{matrix}
A=\frac{9}{14}\\
B=\frac{2}{7}\\
C=\frac{1}{14}
\end{matrix}
\right.
$

(5)平稳分布的熵是多少？

一个概率分布的熵由下式给出：
$$ H_p(x) = E[-log_2p(x)] $$
可导出：
$$ H_p(x) = - \Sigma_xp(x)log_2p(x) $$
$$ H_p(x) = - \int p(x)log_2p(x)dx $$
平稳分布的熵为：
$ \begin{aligned}
H_p(x) &= -\Sigma_x p(x)log_2 p(x)\\
&= -(\frac{9}{14} \times log_2 (\frac{9}{14})+\frac{2}{7} \times log_2 (\frac{2}{7})+\frac{1}{14} \times log_2 (\frac{1}{14}))\\
&= -(-0.4097763775-0.5163871206-0.271953923)\\
&= 1.198117421
\end{aligned} $

(6)利用贝叶斯准则，计算给定今天天气时昨天天气的概率表。

以今天是晴天为例：
$ \begin{aligned}
p(昨天 = \text{sunny} | 今天 = \text{sunny}) &= \eta p(今天 = \text{sunny} | 昨天 = \text{sunny})p(昨天 = \text{sunny})\\
&= \eta \times 0.8 \times \frac{9}{14}\\
&= \frac{18}{35} \eta\\
p(昨天 = \text{cloudy} | 今天 = \text{sunny}) &= \eta p(今天 = \text{sunny} | 昨天 = \text{cloudy})p(昨天 = \text{cloudy})\\
&= \eta \times 0.4 \times \frac{2}{7}\\
&= \frac{4}{35} \eta\\
p(昨天 = \text{rainy} | 今天 = \text{sunny}) &= \eta p(今天 = \text{sunny} | 昨天 = \text{sunny})p(昨天 = \text{sunny})\\
&= \eta \times 0.2 \times \frac{1}{14}\\
&= \frac{1}{70} \eta\\
\end{aligned} $
$ \begin{aligned}
\frac{18}{35} \eta + \frac{4}{35} \eta + \frac{1}{70} \eta = 1 \rightarrow \eta = \frac{14}{9}
\end{aligned} $
$ \begin{aligned}
p(昨天 = \text{sunny} | 今天 = \text{sunny}) &= \frac{4}{5}\\
p(昨天 = \text{cloudy} | 今天 = \text{sunny}) &= \frac{8}{45}\\
p(昨天 = \text{rainy} | 今天 = \text{sunny}) &= \frac{1}{45}
\end{aligned} $

(7)假设将季节加入到该模型中。上面的状态转移函数仅能应用于夏天，而不同的模型将应用于冬天、春天和秋天。这会扰乱这个过程的马尔科夫特性吗？

马尔可夫特性：当一个随机过程在给定现在状态及所有过去状态情况下，其未来状态的条件概率分布仅依赖于当前状态；换句话说，在给定现在状态时，它与过去状态（即该过程的历史路径）是条件独立的，那么此随机过程即具有马尔可夫性质。
在本例中，虽然状态转移矩阵会随季节而变化，但仍然是已知的。下一天的天气条件概率分布仅依赖于前一天的天气，因此该过程具有马尔可夫性质。

3.在第二题的基础上，假设不能直接观测天气，但是可以依靠传感器。问题是传感器本身是有噪声的。其测量受到下面的测量模型控制：

实际天气	传感器观测
	晴	多云	雨
晴	0.6	0.4	0
多云	0.3	0.7	0
雨	0	0	1

今天	明天
	晴	多云	雨
晴	0.8	0.2	0
多云	0.4	0.4	0.2
雨	0.2	0.6	0.2

(1)设第一天是晴（这是一个已知事实），传感器观测到的接下来的4天为多云、多云、雨、晴，则第五天用传感器预测为晴的概率是多少？

待求量可写成：$ p(X_5 = \text{sunny}|z_{2:5},x_1) $
先从简单入手，即第二天用传感器预测为晴的概率：
待求量为：$ p(X_2 = \text{sunny}|x_1) $
由贝叶斯准则：
$ \begin{aligned}
p(X_2 = \text{sunny}|z_2,x_1) &= \eta p(z_2|X_2 = \text{sunny},x_1) p(X_2=\text{sunny}|x_1)\\
&= \eta p(z_2|X_2=\text{sunny})p(X_2=\text{sunny}|x_1)
\end{aligned} $
然后是第三天，由贝叶斯准则：
$$ p(x|y,z) = \frac{p(y|x,z)p(x|z)}{p(y|z)} $$
得到：
$ \begin{aligned}
&p(X_3 = \text{sunny}|z_{2:3},x_1) = p(X_3 = \text{sunny}|z_2,z_3,x_1)\\
&= \eta p(z_3|z_2,X_3 = \text{sunny},x_1) p(X_3=\text{sunny}|z_2,x_1) \\
&= \eta p(z_3|X_3 = \text{sunny}) \Sigma_{w}^{sunny,cloudy,rainy} p(X_3=\text{sunny}|X_2=\text{w})p(X_2 = \text{w}|z2,x1)
\end{aligned} $
上式需要解释的是：第一行中把两个观测量拆开以便用贝叶斯准则。第三行，因为第二天的观测和第一天的实际值对第三天的观测没有影响(第三天的观测只与第三天的实际值有关)，因此可以舍去一些不必要的参数；第三项可以与第二天的概率建立练习，具体来说就是把第二天的概率乘以状态转移函数，这一步要求和，因为第二天的三种天气都与第三天的晴有概率关系。
总结上述两天即可建立迭代关系：
$ \begin{aligned}
&p(X_n = \text{sunny}|z_{2:n},x_1) \\
&= \eta p(z_n|z_{2:n-1},X_n = \text{sunny},x_1) p(X_n=\text{sunny}|z_{2:n-1},x_1) \\
&= \eta p(z_n|X_n = \text{sunny}) \Sigma_{w}^{sunny,cloudy,rainy} p(X_n=\text{sunny}|X_{n-1}=\text{w}) p(X_{n-1} = \text{w}|z_{2:n-1},x1)
\end{aligned} $
观察表格发现，传感器观测结果为雨时不会出错，也就是说，第四天的实际天气为雨。所以第四天前的迭代是没有意义的。因此可以直接算第五天：
$ \begin{aligned}
&p(X_5 = \text{sunny}|z_{2:5},x_1) \\
&= \eta p(z_5|X_5 = \text{sunny}) \Sigma_{w}^{sunny,cloudy,rainy} p(X_5=\text{sunny}|X_{4}=\text{w}) p(X_{4} = \text{w}|z_{2:4},x1)\\
&= \eta \times 0.6 \times (0.8 \times 0 + 0.4 \times 0 + 0.2 \times 1)\\
&= 0.12 \eta
\end{aligned} $
$ \begin{aligned}
&p(X_5 = \text{cloudy}|z_{2:5},x_1) \\
&= \eta p(z_5|X_5 = \text{cloudy}) \Sigma_{w}^{sunny,cloudy,rainy} p(X_5=\text{cloudy}|X_{4}=\text{w}) p(X_{4} = \text{w}|z_{2:4},x1)\\
&= \eta \times 0.3 \times (0.2 \times 0 + 0.4 \times 0 + 0.6 \times 1)\\
&= 0.18 \eta
\end{aligned} $
$ \begin{aligned}
&p(X_5 = \text{rainy}|z_{2:5},x_1) \\
&= \eta p(z_5|X_5 = \text{rainy}) \Sigma_{w}^{sunny,cloudy,rainy} p(X_5=\text{rainy}|X_{4}=\text{w}) p(X_{4} = \text{w}|z_{2:4},x1)\\
&= 0 \eta
\end{aligned} $
$ \begin{aligned}
&\eta = \frac{10}{3}\\
&p(X_5 = \text{sunny}|z_{2:5},x_1) = 0.4\\
&p(X_5 = \text{cloudy}|z_{2:5},x_1) = 0.6
\end{aligned} $
可以用如下程序表示该运算：

import numpy as np

ans = np.array([1,0,0])
K = np.array([[0.8,0.2,0],[0.4,0.4,0.2],[0.2,0.6,0.2]])
Z = np.array([[0.6,0.3,0],[0.4,0.7,0],[0,0,1]])
weather = [1,1,2,0]

for w in weather:
    ans=np.dot(ans,K)
    ans[0]=ans[0]*Z[w][0]
    ans[1]=ans[1]*Z[w][6]
    ans[2]=ans[2]*Z[w][7]
    eta = 1/(ans[0]+ans[1]+ans[2])
    ans = np.dot(ans,eta)
    print(ans)

结果如下：
[0.69565217 0.30434783 0. ]
[0.59770115 0.40229885 0. ]
[0. 0. 1.]
[0.4 0.6 0. ]

(2)再一次，假定已知第一天是晴。在第2-4天，传感器测量为晴、晴、雨。对第2-4天，当天最可能的天气是怎样的？用两种方式回答问题：一种是只有讨论那天的数据是可用的；另一种是基于后见之明的，未来几天的数据也是可用的。

(3)考虑同一种情况（第一天晴、第2-4天分别是晴、晴、雨）。对第2-4天的天气最有可能是什么样的？这个最可能序列的概率是多少？

第一种方式与上一问的方法一样，只需要设置$ weather = [0,0,2] $即可。
结果如下：
[0.88888889 0.11111111 0. ]
[0.87179487 0.12820513 0. ]
[0. 0. 1.]

对于第二种方式，仍然需要总结出可以迭代的方法，因此第n天的概率表达式中可以确定有一项必为n-1天的概率。
$ \begin{aligned}
&p(X_n = \text{sunny}|z_{2:4},x_1) = \Sigma_w^{sunny,cloudy,rainy} p(X_n=\text{sunny}|X_{n-1}=w,z_{2:4},x_1) p(X_{n-1}=w|z_{2:4},x_1)\\
&p(X_n=\text{sunny}|X_{n-1}=w,z_{2:4},x_1)=\eta p(z_{2:4}|X_n=\text{sunny},X_{n-1}=w) p(X_n=\text{sunny}|X_{n-1}=w)
\end{aligned} $
注意到：
$ \begin{aligned}
p(X_1 |z_{2:4},x_1) &= (1,0,0)
\end{aligned} $
对于第2天，因为$x_1=\text{sunny}$，所以$w=sunny$，其他项为0，有：
$ \begin{aligned}
p(X_2=\text{sunny}|z_{2:4},x_1)&=\eta p(z_{2:4}|X_2=\text{sunny},X_1=sunny) p(X_2=\text{sunny}|X_1=sunny)\\
&=\eta \times 0.6 \times 1 \times 0.8\\
&=0.48 \eta = \frac{24}{27}
\end{aligned} $
$ \begin{aligned}
p(X_2=\text{cloudy}|z_{2:4},x_1)&=\eta p(z_{2:4}|X_2=\text{cloudy},X_1=sunny) p(X_2=\text{cloudy}|X_1=sunny)\\
&=\eta \times 0.3 \times 1 \times 0.2\\
&=0.06 \eta = \frac{1}{9}
\end{aligned} $
$ \begin{aligned}
p(X_2=\text{rainy}|z_{2:4},x_1)&=\eta p(z_{2:4}|X_2=\text{rainy},X_1=sunny) p(X_2=\text{cloudy}|X_1=sunny)\\
&=0 \eta = 0
\end{aligned} $
$ \begin{aligned}
\eta = \frac{50}{27}
\end{aligned} $
对于第三天：
$ \begin{aligned}
p(X_3=\text{sunny}|z_{2:4},x_1)&=\eta \Sigma p(z_{2:4}|X_3=\text{sunny},X_2=w) p(X_3=\text{sunny}|X_2=w) p(X_2=w|z_{2:4},x_1)\\
&=\eta \times 0.6 \times (0.8 \times 0.6 \times \frac{24}{27} + 0.4 \times 0.3 \times \frac{1}{9} + 0.2 \times 0 \times 0)\\
&=0.264 \eta = 0.88
\end{aligned} $
$ \begin{aligned}
p(X_3=\text{cloudy}|z_{2:4},x_1)&=\eta \Sigma p(z_{2:4}|X_3=\text{cloudy},X_2=w) p(X_3=\text{cloudy}|X_2=w)p(X_2=w|z_{2:4},x_1)\\
&=\eta \times 0.3 \times (0.2 \times 0.6 \times \frac{24}{27} + 0.4 \times 0.3 \times \frac{1}{9} + 0.6 \times 0 \times 0)\\
&=0.036 \eta = 0.12
\end{aligned} $
$ \begin{aligned}
p(X_3=\text{rainy}|z_{2:4},x_1)&=\eta \Sigma p(z_{2:4}|X_3=\text{rainy},X_2=w) p(X_3=\text{rainy}|X_2=w)p(X_2=w|z_{2:4},x_1)\\
&=\eta \times 0 \times (0 \times 0.6 \times \frac{24}{27} + 0.2 \times 0.3 \times \frac{1}{9} + 0.2 \times 0 \times 0)\\
&=0
\end{aligned} $
$ \begin{aligned}
\eta = \frac{10}{3}
\end{aligned} $
对于第四天，测量为雨因此必为雨。所以可得：
$ \begin{aligned}
p(X_4=\text{sunny}|z_{2:4},x_1)=0
\end{aligned} $
$ \begin{aligned}
p(X_4=\text{cloudy}|z_{2:4},x_1)=0
\end{aligned} $
$ \begin{aligned}
p(X_4=\text{rainy}|z_{2:4},x_1)=1
\end{aligned} $

4.在这个练习中把贝叶斯准则应用到高斯情况。假设是一个位于长直道路上的移动机器人，位置x是简单地沿着这条路的某个位置。现在假设最初位置$ x_{init}=1000m $，碰巧指导这个估计是不确定的。基于这种不确定性，用高斯建立方差为$ \sigma_{init}^2 = 900m^2 $的初始置信度模型。为了得到关于位置的更多信息，查询一个GPS接收器。GPS告诉位置是$ z_{GPS} = 1100m $。已知该GPS接收器的误差方差为$ \sigma_{init}^2 = 100m^2 $。

(1)写出先验$p(x)$和测量$p(z|x)$的概率密度函数。

$ p(x) = (2 \pi \sigma^2)^{-\frac{1}{2}} exp \{-\frac{1}{2}\frac{(x-\mu)^2}{\sigma^2}\}=(1800\pi)^{-\frac{1}{2}}exp\{-\frac{1}{2}\frac{(x-1000)^2}{900}\}\\
p(z|x) = (2 \pi \sigma^2)^{-\frac{1}{2}} exp \{-\frac{1}{2}\frac{(x-\mu)^2}{\sigma^2}\}=(200\pi)^{-\frac{1}{2}}exp\{-\frac{1}{2}\frac{(z-x)^2}{100}\} $

(2)使用贝叶斯准则，后验$ p(x|z) $是多少？证明它是一个高斯分布。

$ \begin{aligned}
p(z) &= \int p(z|x)p(x)dx\\
&= \frac{1}{2\pi \times 30 \times 10} \int exp\{ -\frac{1}{2}(\frac{(z-x)^2}{100}+\frac{(x-1000)^2}{900}) \}dx
\end{aligned} $

因为$p(z)$不依赖x，因此$p(z)^{-1}$可以被写为归一化变量$\eta$。

$ \begin{aligned}
p(x|z) &= \frac{p(z|x)p(x)}{p(z)}\\
&= (200\pi)^{-\frac{1}{2}}exp\{-\frac{1}{2}\frac{(z-x)^2}{100}\} \times (1800\pi)^{-\frac{1}{2}}exp\{-\frac{1}{2}\frac{(x-1000)^2}{900}\} \times \eta\\
\end{aligned} $
$ p(x|z) $显然符合高斯分布。

(3)测量$ x_{GPS}=1100m $怎样得出先验和GPS接收器的误差概率信息？

$ \begin{aligned}
p(x) &= (2 \pi \sigma^2)^{-\frac{1}{2}} exp \{-\frac{1}{2}\frac{(x-\mu)^2}{\sigma^2}\}\\
&=(1800\pi)^{-\frac{1}{2}}exp\{-\frac{1}{2}\frac{(x-1000)^2}{900}\}\\
&=(1800\pi)^{-\frac{1}{2}}exp\{-\frac{1}{2}\frac{(1100-1000)^2}{900}\}\\
&=\frac{1}{30\sqrt{2\pi}}e^{-\frac{50}{9}}
\end{aligned} $
$ \begin{aligned}
p(z|x) &= (2 \pi \sigma^2)^{-\frac{1}{2}} exp \{-\frac{1}{2}\frac{(x-\mu)^2}{\sigma^2}\}\\
&=(200\pi)^{-\frac{1}{2}}exp\{-\frac{1}{2}\frac{(z-x)^2}{100}\} \\
&=(200\pi)^{-\frac{1}{2}}exp\{-\frac{1}{2}\frac{(1100-1100)^2}{100}\}\\
&=0
\end{aligned} $

5.由$$p(x,y|z)=p(x|z)p(y|z)$$推导$$p(x|z)=p(x|z,y)\\p(y|z)=p(y|z,x)$$

根据条件概率定义：
$$ p(x|y)=\frac{p(x,y)}{p(y)}$$
得到：$p(x,y|z)=p(y|z)p(x|y,z)=p(x|z)p(y|x,z)$
消去相同项即可得证。

6.证明协方差公式$$Cov[X]=E[X-E[X]]^2=E[X^2]-E[X]^2$$

$ \begin{aligned}
Cov(X)&=E{[X-E(X)]^2}\\
&=E(X^2)-2XE(X)+[E(X)]^2\\
&=E(X^2)-2E(X)E(X)+[E(X)]^2\\
&=E(X^2)-[E(X)]^2
\end{aligned} $