第四章

1.在本习题中，请对前面章节研究的线性动态系统进行一个直方图滤波实现。

(1)对这本书第3章习题1所描述的动态系统进行直方图滤波实现。利用滤波为时刻$t(t=1,2,\cdot,5)$的每个值预测后验分布。绘制关于$x$和$x^{'}$的联合后验，这里$x$为横轴，$x^{'}$为纵轴。

(引用3.1)在本题及下面的练习中，请为一个简单的动态系统——在线性环境中按线性动态运动的汽车，设计一个卡尔曼滤波。为了简单起见，假定$\Delta t = 1$。t时刻汽车的位置由$x_t$给定。其速度为$\dot{x}_t$，加速度为$\ddot{x}_t$；符合均值为0，协方差为$\sigma^2=1$的高斯分布，假定可以任意设定每个时间点的加速度。

离散贝叶斯滤波：
$
Algorithm~Discrete\_Bayes\_filter({p_{k,t-1}},u_t,z_t):$
  $for~all~k~do$
    $\bar{p}_{k,t}=\sum_i p(X_t=x_k|u_t,X_{t-1}=x_i) p_{i,t-1}$
    $p_{k,t}=\eta p(z_t|X_t=x_k)\bar{p}_{k,t}$
  $endfor$
  $return~\{p_{k,t}\}$

加速度符合均值为0，协方差为1的高斯分布。
$p(x)=(2\pi\sigma^2)^{-\frac{1}{2}} exp\{-\frac{1}{2} \frac{(x-\mu)^2}{\sigma^2}\}
=\frac{e^{-\frac{1}{2}x^2}}{\sqrt{2\pi}}$
对该函数采样：

import matplotlib.pyplot as plt
import numpy as np
import math

a = np.linspace(-5, 5, 50)
pa = np.exp(-1/2*a*a)/np.sqrt(2*np.pi)
plt.plot(a,pa)

#采样
xx = np.linspace(-2, 2, 5)
pxx = np.exp(-1/2*xx*xx)/np.sqrt(2*np.pi)
#归一化
pxx_sum = 1/np.sum(pxx)
pxx = np.dot(pxx_sum,pxx)

plt.bar(xx,pxx,color='purple',alpha=0.3)
print(pxx)
plt.show()

得到概率分布：

a	-2	-1	0	1	2
p(a)	0.05448868	0.24420134	0.40261995	0.24420134	0.05448868

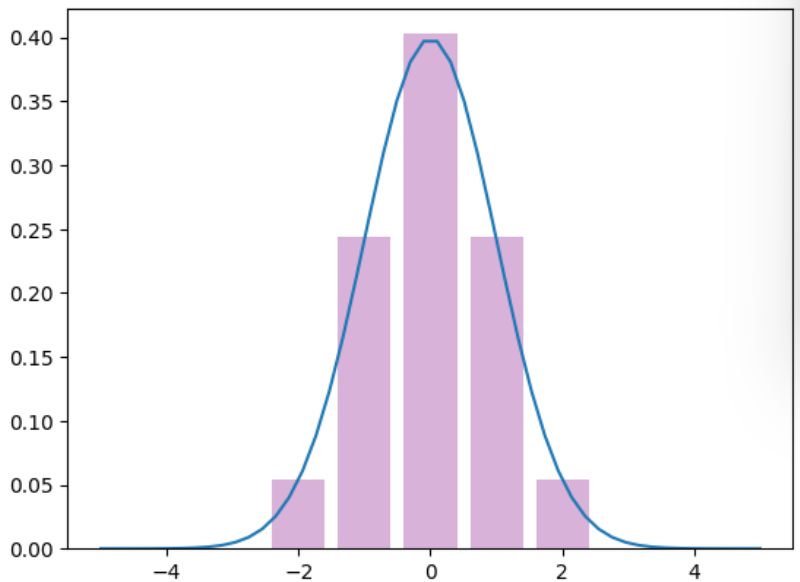
$v$的概率分布：
$t=1$时：
$pv[1]=\begin{pmatrix}0.05448868 & 0.24420134 & 0.40261995 & 0.24420134 & 0.05448868\end{pmatrix}$
$t=2$时：
$pv[2][-4]=pv[1][-2]pa[-2]$
$pv[2][-3]=pv[1][-2]pa[-1]+pv[1][-1]pa[-2]$
$pv[2][-2]=pv[1][-2]pa[0]+pv[1][-1]pa[-1]+pv[1][0]pa[-2]$
$pv[2][-1]=pv[1][-2]pa[1]+pv[1][-1]pa[0]+pv[1][0]pa[-1]+pv[1][2]pa[-2]$
$pv[2][0]=pv[1][-2]pa[2]+pv[1][-1]pa[1]+pv[1][0]pa[0]+pv[1][3]pa[-1]+pv[1][4]pa[-2]$
其余部分概率分布与上述部分对称。
只选择-2到2的区间进行迭代。

import matplotlib.pyplot as plt
import numpy as np
import math

p=np.array([[0.05448868,0.24420134,0.40261995,0.24420134,0.05448868],\
            [0,0,0,0,0],\
            [0,0,0,0,0],\
            [0,0,0,0,0],\
            [0,0,0,0,0]])
pa=np.array([0.05448868,0.24420134,0.40261995,0.24420134,0.05448868,0,0,0,0,0,0,0,0,0])
for t in range(1,5):
    p[t][0]=p[t-1][0]*pa[2]+p[t-1][5]*pa[1]+p[t-1][6]*pa[0]
    p[t][7]=p[t-1][0]*pa[3]+p[t-1][8]*pa[2]+p[t-1][9]*pa[1]+p[t-1][10]*pa[0]
    p[t][11]=p[t-1][0]*pa[4]+p[t-1][12]*pa[3]+p[t-1][13]*pa[2]+p[t-1][14]*pa[1]+p[t-1][15]*pa[0]
    p[t][16]=p[t][17]
    p[t][18]=p[t][0]
    psum=0
    for i in range(0,5):
        psum=psum+p[t][i]
    for i in range(0,5):
        p[t][i]=1/psum*p[t][i]
        #print(p[t][i])
    plt.bar(xx,p[t],color='purple',alpha=0.3)
    plt.show()
print(p)

直方图如图所示，所得概率矩阵为：

	v=-2	v=-1	v=0	v=1	v=2
t=1	0.05448868	0.24420134	0.40261995	0.24420134	0.05448868
t=2	0.10593992	0.23732692	0.31346633	0.23732692	0.10593992
t=3	0.12648582	0.23112599	0.28477638	0.23112599	0.12648582
t=4	0.13448707	0.22873842	0.27354903	0.22873842	0.13448707
t=5	0.13768919	0.22778266	0.26905629	0.22778266	0.13768919

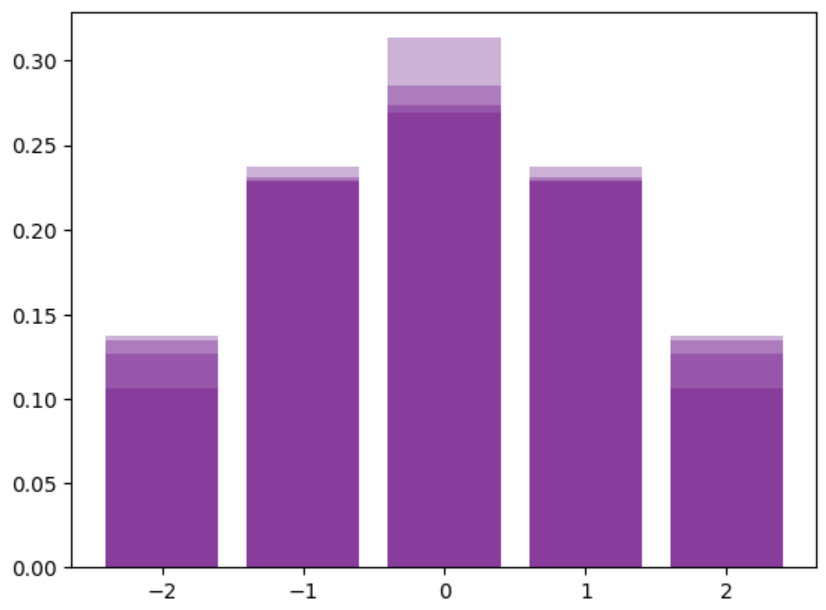
对于$x$：

px=np.array([[0.05448868,0.24420134,0.40261995,0.24420134,0.05448868],\
            [0,0,0,0,0],\
            [0,0,0,0,0],\
            [0,0,0,0,0],\
            [0,0,0,0,0]])
for t in range(1,5):
    px[t][0]=px[t-1][0]*p[t][20]+px[t-1][21]*p[t][22]+px[t-1][23]*p[t][0]
    px[t][24]=px[t-1][0]*p[t][25]+px[t-1][26]*p[t][27]+px[t-1][28]*p[t][29]+px[t-1][30]*p[t][0]
    px[t][31]=px[t-1][0]*p[t][32]+px[t-1][33]*p[t][34]+px[t-1][35]*p[t][36]+px[t-1][37]*p[t][38]+px[t-1][39]*p[t][0]
    px[t][40]=px[t][41]
    px[t][42]=px[t][0]
    pxsum=0
    for i in range(0,5):
        pxsum=pxsum+px[t][i]
    for i in range(0,5):
        px[t][i]=1/pxsum*px[t][i]
        #print(p[t][i])
    plt.bar(xx,px[t],color='purple',alpha=0.3)
print(px)

直方图如图所示，概率矩阵为：

	x=-2	x=-1	x=0	x=1	x=2
t=1	0.05448868	0.24420134	0.40261995	0.24420134	0.05448868
t=2	0.12920832	0.231546	0.27849136	0.231546	0.12920832
t=3	0.14786234	0.22314876	0.2579778	0.22314876	0.14786234
t=4	0.15156189	0.22086468	0.25514688	0.22086468	0.15156189
t=5	0.15236539	0.22027755	0.25471414	0.22027755	0.15236539

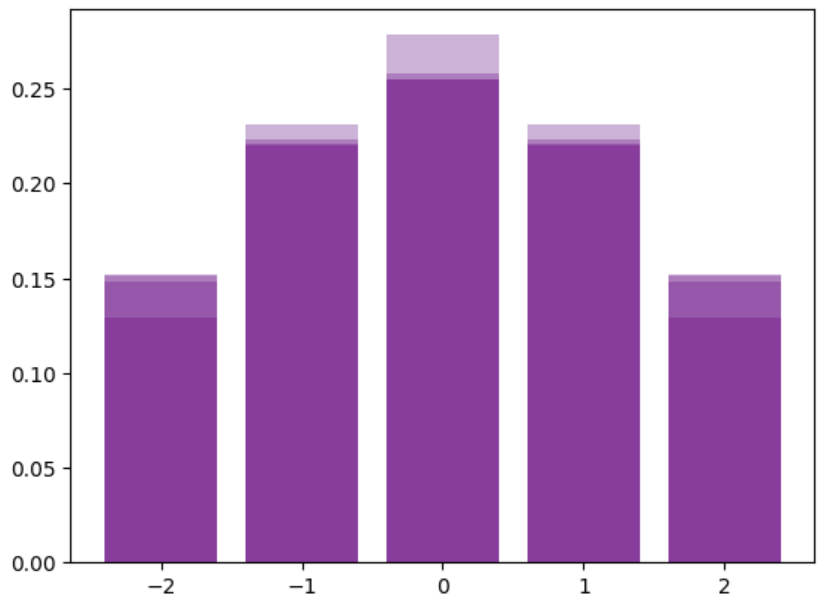
(2)在直方图滤波中，如本书第3章的习题2所描述的测量更新步骤，假定在时刻$t=5$，观测到一个测量$z=5$。在更新直方图滤波之前和之后说明和绘制后验。

$Algorithm~Discrete\_Bayes\_filter({p_{k,t-1}},u_t,z_t):$
  $for~all~k~do$
    $\bar{p}_{k,t}=\sum_i p(X_t=x_k|u_t,X_{t-1}=x_i) p_{i,t-1}$
    $p_{k,t}=\eta p(z_t|X_t=x_k)\bar{p}_{k,t}$
  $endfor$
  $return~\{p_{k,t}\}$

第3章习题2中，测量$z=5$，协方差$\sigma^2=10$的高斯噪声。因为本题中简化计算让$x$在$(-2,2)$之间，因此令$z=0$以便简化计算。

$p(z)=(2\pi\sigma^2)^{-\frac{1}{2}} exp\{-\frac{1}{2} \frac{(z-\mu)^2}{\sigma^2}\}
=\frac{e^{-\frac{1}{2}\frac{(z-5)^2}{10}}}{2\sqrt{5\pi}}$

import matplotlib.pyplot as plt
import numpy as np
import math

a = np.linspace(0, 10, 50)
pa = np.exp(-1/20*(a-5)*(a-5)) / np.sqrt(20*np.pi)
plt.plot(a,pa)

#采样
xx = np.linspace(3, 7, 5)
pxx = np.exp(-1/20*(xx-5)*(xx-5)) / np.sqrt(20*np.pi)
#归一化
pxx_sum = 1/np.sum(pxx)
pxx = np.dot(pxx_sum,pxx)

plt.bar(xx,pxx,color='purple',alpha=0.3)
print(pxx)
plt.show()

测量的直方图如图所示，概率矩阵为：

z	-2	-1	0	1	2
p(z)	0.18034033	0.20952558	0.22026818	0.20952558	0.18034033

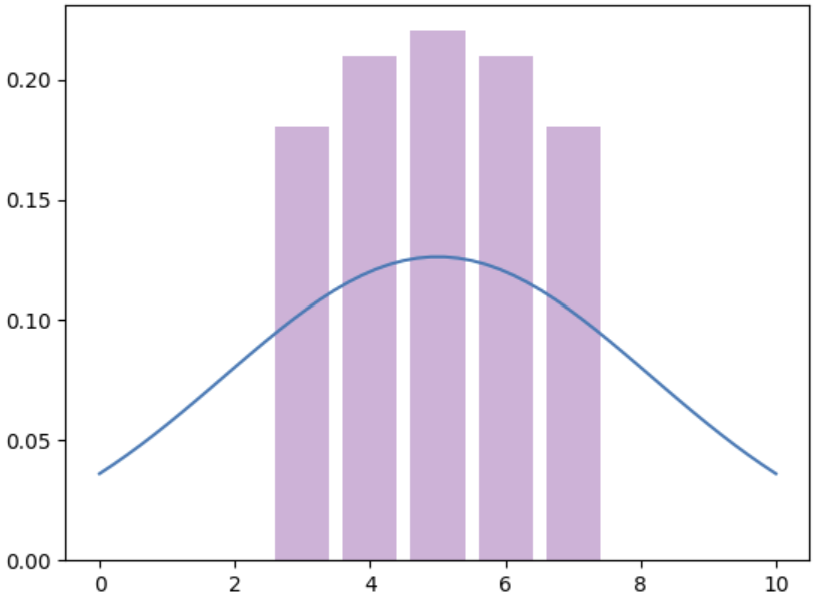
$p_{5} = \eta p(z|x)\bar{p}_5 $

ans = np.zeros(5)
psum = 0
for t in range(0,5):
    ans[t]=pxx[t]*px[4][t]
    psum = psum + ans[t]
for t in range(0,5):
    ans[t] = ans[t]/psum
print(ans)

x	-2	-1	0	1	2
p(x)	0.13511267	0.22694685	0.27588095	0.22694685	0.13511267

2.对本书第3章习题4研究的非线性进行直方图滤波实现。这里，研究的是一个具有3个状态变量并具有确定的状态转移的非线性系统。

$$\begin{pmatrix}
x^{'}\\ y^{'}\\ \theta^{'}
\end{pmatrix}=\begin{pmatrix}
x+cos\theta \\ y+sin\theta \\ \theta
\end{pmatrix}$$

初始状态估计如下：

$$\mu=\begin{pmatrix}
0&0&0
\end{pmatrix},
\Sigma = \begin{pmatrix}
0.01 & 0 & 0 \\
0 & 0.01 & 0 \\
0 & 0 & 10000
\end{pmatrix}$$

(1)为直方图滤波建立一个合适的初始估计，它反映高斯先验的状态信息。

import matplotlib.pyplot as plt
import numpy as np
import math

a = np.linspace(-5, 5, 100)
pa = np.exp(-1/0.2*(a)*(a)) / np.sqrt(0.2*np.pi)
plt.plot(a,pa)

#采样
xx = np.linspace(-1, 1, 5)
pxx = np.exp(-1/0.2*(xx)*(xx)) / np.sqrt(0.2*np.pi)
#归一化
pxx_sum = 1/np.sum(pxx)
pxx = np.dot(pxx_sum,pxx)

plt.bar(xx,pxx,color='purple',alpha=0.3,width=0.3)
print(pxx)
plt.show()

a = np.linspace(-10, 10, 100)
pa = np.exp(-1/200*(a)*(a)) / np.sqrt(200*np.pi)
plt.plot(a,pa)

#采样
xx = np.linspace(-np.pi, np.pi, 9)
pxx = np.exp(-1/200*(xx)*(xx)) / np.sqrt(200*np.pi)
#归一化
pxx_sum = 1/np.sum(pxx)
pxx = np.dot(pxx_sum,pxx)

plt.bar(xx,pxx,color='purple',alpha=0.3,width=0.3)
print(pxx)
plt.show()

对于$x$和$y$：

x,y	-1	-0.5	0	0.5	1
p	0.00424709	0.18059087	0.63032408	0.18059087	0.00424709

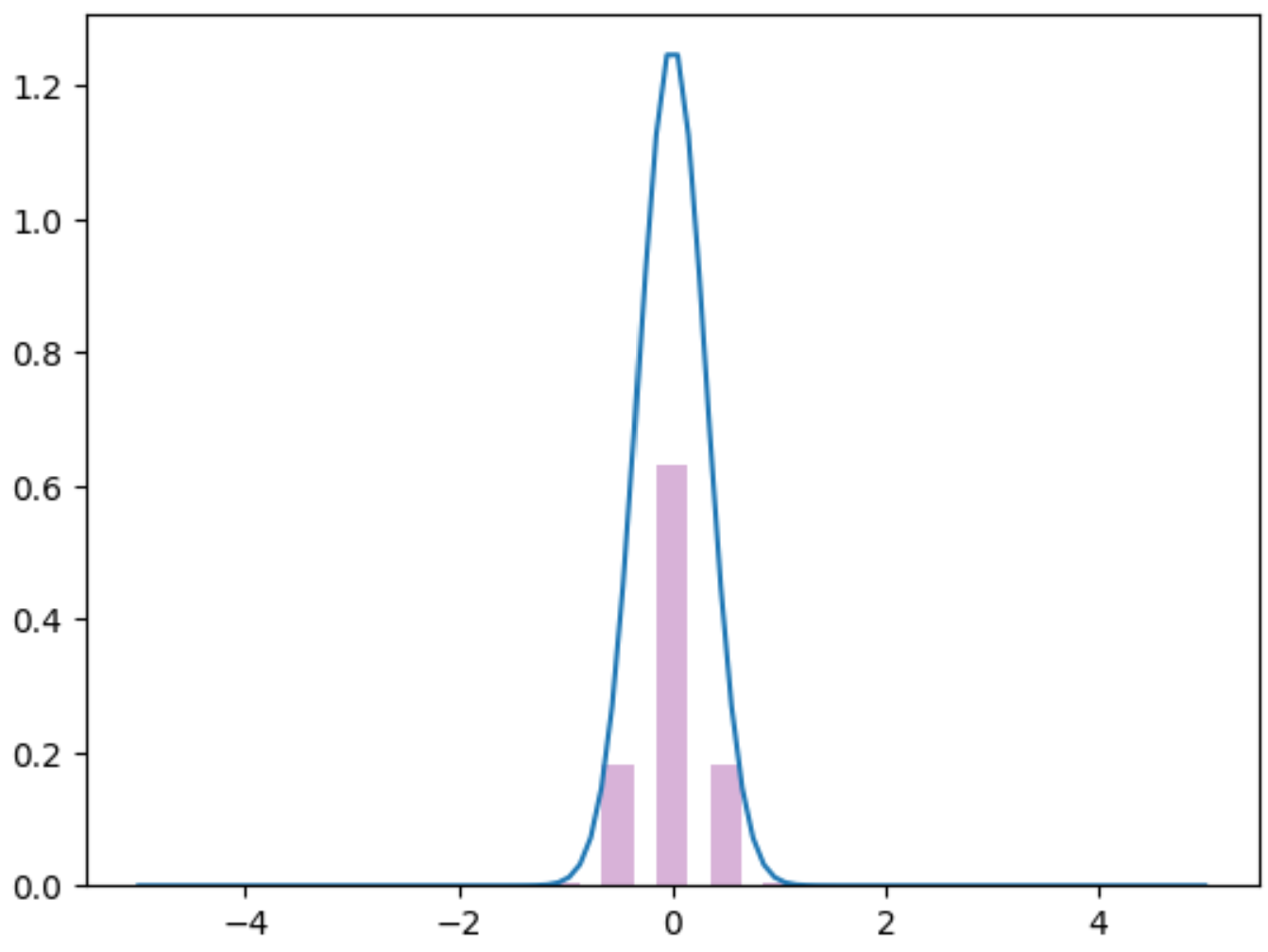
对于$\theta$：

$\theta$	$-\pi$	$-\frac{3}{4}\pi$	$-\frac{1}{2}\pi$	$-\frac{1}{4}\pi$	0
p	0.10794071	0.11029646	0.11201056	0.11305177	0.11340099

$\theta$	0	$\frac{1}{4}\pi$	$\frac{1}{2}\pi$	$\frac{3}{4}\pi$	$\pi$
p	0.11340099	0.11305177	0.11201056	0.11029646	0.10794071

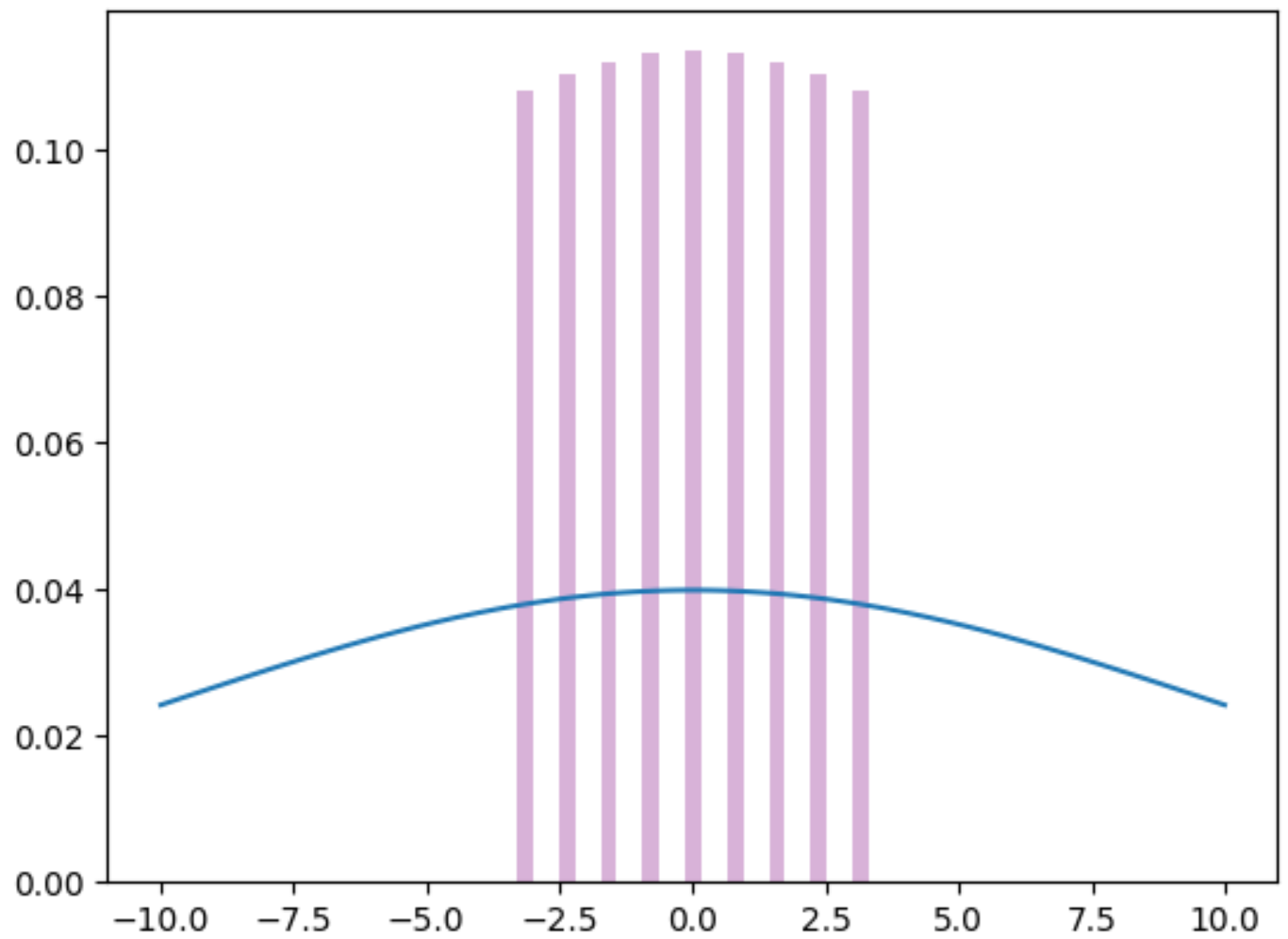
(2)实现直方图滤波并执行其预测步骤。

import matplotlib.pyplot as plt
import numpy as np
import math

pxy=np.array([0.00424709,0.18059087,0.63032408,0.18059087,0.00424709])
ptheta=np.array([0.10794071,0.11029646,0.11201056,0.11305177,0.11340099,0.11305177,0.11201056,0.11029646,0.10794071])

pxy1=np.zeros(5)

for i in range(0,5):
    for j in range(0,5):
        pxy1[i]=pxy1[i]+pxy[j]*ptheta[4+i-j]

#归一化
sum = 1/np.sum(pxy1)
pxy1 = np.dot(sum,pxy1)

print(pxy1)

x,y	-1	-0.5	0	0.5	1
p	0.19877045	0.20061364	0.20123183	0.20061364	0.19877045

(3)将测量归并入估计。测量是机器人坐标$x$的有噪声映射，协方差为$Q=0.01$。执行这一步骤，计算出结果并绘图。

#采样
xx = np.linspace(-1, 1, 5)
pxx = np.exp(-1/0.2*(xx)*(xx)) / np.sqrt(0.2*np.pi)
#归一化
pxx_sum = 1/np.sum(pxx)
pxx = np.dot(pxx_sum,pxx)
print(pxx)

for i in range(0,5):
    pxy1[i]=pxy1[i]*pxx[i]

#归一化
sum = 1/np.sum(pxy1)
pxy1 = np.dot(sum,pxy1)

print(pxy1)

x,y	-1	-0.5	0	0.5	1
p	0.00420024	0.18025482	0.63108988	0.18025482	0.00420024

3.本章讨论了使用单一粒子的效果。粒子滤波时粒子数$M=2$时效果如何？能给出一个影响偏差的例子吗？如果有，是怎样的？

$
Algorithm~Partical\_filter(\chi_{t-1},u_t,z_t):$
  $\bar{\chi}_t=\chi_t=\emptyset$
  $for~m=1~toM~do$
    $sample~x_t^{[m]}\sim p(x_t|u_t,x_{t-1}^{[m]})$
    $w_t^{[m]}=p(z_t|x_t^{[m]})$
    $\bar{\chi}_t=\bar{\chi}_t+<x_t^{[m]},w_t^{[m]}>$
  $endfor$
  $for~m=1~to~M~do$
    $draw~i~with~probability~\propto~w_t^{[i]}$
    $add~x_t^{i}~to~\chi_t$
  $endfor$
  $return~\chi_t$
如果粒子数为1：
$
Algorithm~Partical\_filter(\chi_{t-1},u_t,z_t):$
  $\bar{\chi}_t=\chi_t=\emptyset$
  $sample~x_t\sim p(x_t|u_t,x_{t-1})$
  $w_t=p(z_t|x_t)$
  $\bar{\chi}_t=\bar{\chi}_t+<x_t,w_t>$
  $draw~1~with~probability~\propto~w_t$
  $add~x_t~to~\chi_t$
  $endfor$
  $return~\chi_t$
在$M=1$这种极端情况下，粒子集中仅包含一个粒子，重采样步骤一定会采用该样本，而不管它的重要性因子为多大。因此测量概率对更新结果不起作用，换言之，它忽略了所有的测量。
当$M=2$，重要性因子可以影响重采样结果，因此测量被加入后验概率的估计中。但是，粒子数较小仍会造成误差较大。M越大越趋近于真实分布，M越小精度越低。

4.用粒子滤波而不是直方图对习题1进行实现，并绘制和讨论结果。

import numpy as np
import matplotlib.pyplot as plt

# 定义状态转移函数和观测函数
def f(x, dt):
    return x  # 假设状态转移函数为x
def h(x):
    return x  # 假设观测函数为x

# 初始化粒子集合和权重集合
N = 100  # 粒子数量
dt = 1   # 时间步长
x = 0    # 初始状态
particles = np.random.randn(N)  # 初始粒子集合
weights = np.ones(N) / N  # 初始权重集合

for t in range(5):  # 迭代5次
    # 状态转移
    plt.scatter(particles,weights)
    plt.show()
    particles = f(particles, dt)
    weights *= np.exp(-1/2 * (particles ** 2) / np.sqrt(2*np.pi))
    # weights *= np.exp(-0.5 * ((z - particles) ** 2) / (0.1 ** 2))
    weights /= np.sum(weights)  # 归一化权重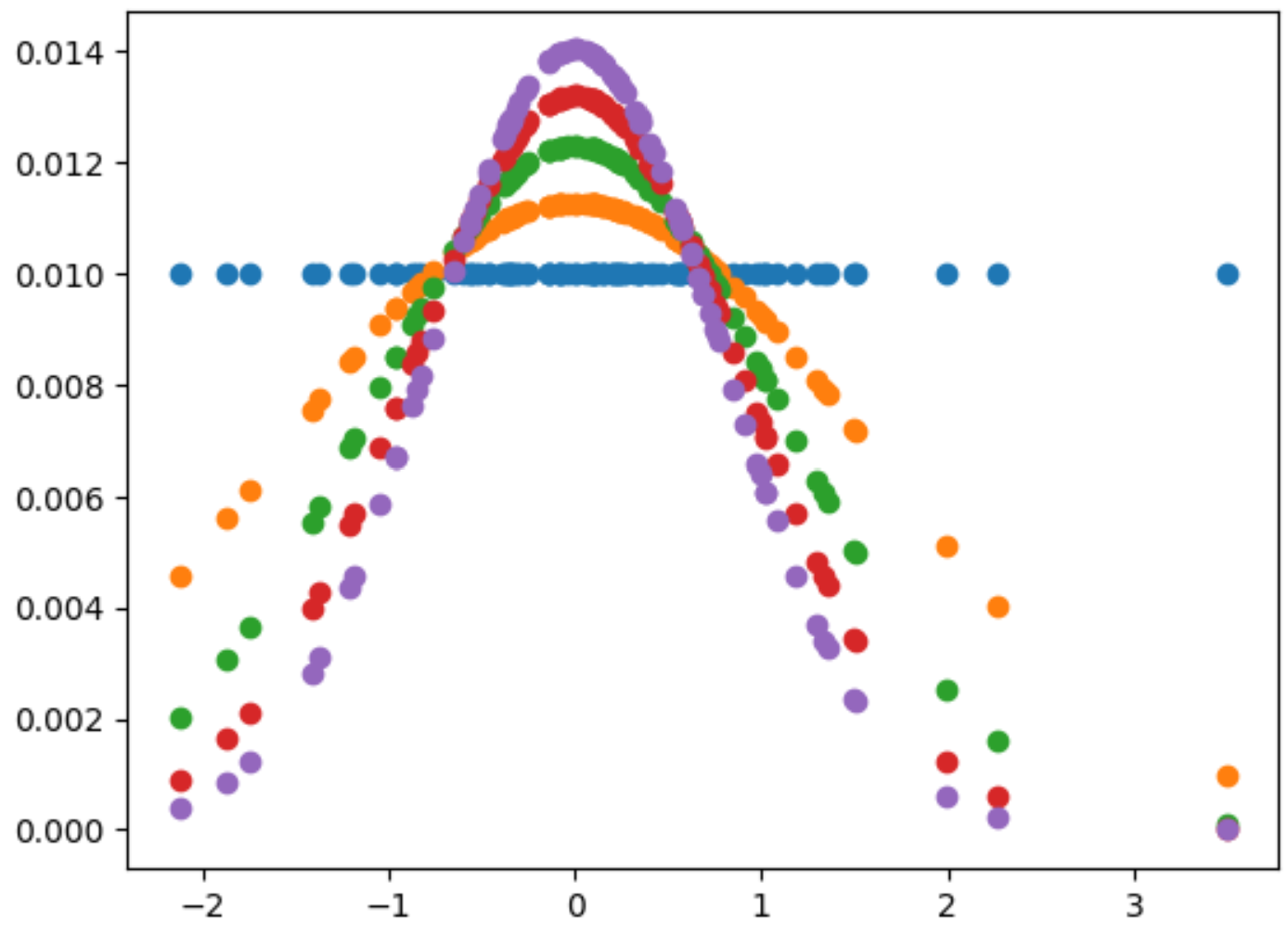

4.用粒子滤波而不是直方图对习题2进行实现，并绘制和讨论结果。研究不同粒子数对结果的影响。

import numpy as np
import matplotlib.pyplot as plt

# 定义状态转移函数和观测函数
def f(x, dt):
    return x + dt * np.cos(np.pi*np.random.randn(100)) # 假设状态转移函数为x

def h(x):
    return x  # 假设观测函数为x

# 初始化粒子集合和权重集合
N = 100  # 粒子数量
dt = 1   # 时间步长
x = 0    # 初始状态
particles = np.random.randn(N)  # 初始粒子集合
weights = np.ones(N) / N  # 初始权重集合

# 高斯噪声
g = np.linspace(-1, 1, 100)
pg = np.exp(-1/0.2*(g)*(g)) / np.sqrt(0.2*np.pi)

for t in range(1):  # 迭代1次
    # 状态转移
    plt.scatter(particles,weights)
    particles = f(particles, dt)
    weights *= np.exp(-1/20 * (particles ** 2) / np.sqrt(20*np.pi))
    weights /= np.sum(weights)  # 归一化权重
    plt.scatter(particles,weights)
    plt.show() 

本题中，因为$\theta$的方差较大，因此在转移中忽略了$x$的方差。结果如图所示：