第五章

1. 本章所有机器人模型都是关于运动学的。本习题中，应将机器人看作是动态（dynamics）的。考虑一个在一维坐标系中的机器人。其位置由$x$表示，$\dot{x}$表示其速度，$\ddot{x}$表示其加速度。假定仅控制加速度$\ddot{x}$。开发一个数学运动模型，计算从初始位姿$x$和速度$\dot{x}$变化到位姿$x'$和速度$\dot{x}'$的后验，假定加速度$\ddot{x}$是给定的加速度和一个具有均值0、方差$\sigma^2$的高斯噪声项之和（并假定实际加速度在仿真间隔$\Delta t$内保持恒定）。$x'$和$\dot{x}'$与后验相关吗？请解释为什么如此或为什么不。

输入：初始状态$X_{t-1} = (x,\dot{x})$，估计后继状态$X_t = (x',\dot{x}')$、控制量$u_t = \ddot{x} + \Delta \ddot{x}$，其中$\Delta \ddot{x} \sim \mathcal{N}(0,\sigma^2)$。
输出：后继状态$X_t$的概率$p(X_t|u_t,X_{t-1})$。

$$ X_t = \begin{pmatrix} x'\\ \dot{x}' \end{pmatrix} = \begin{pmatrix} x + \frac{1}{2}\{2\dot{x}+(\ddot{x}+ \Delta \ddot{x})\Delta t\}\Delta t \\ \dot{x}+(\ddot{x}+ \Delta \ddot{x})\Delta t \end{pmatrix} $$

$$ p(\dot{x}'|u_t,\dot{x}) \sim \mathcal{N}(\dot{x} + \ddot{x} \Delta t,\Delta t^2 \sigma^2) $$

$$ p(x'|u_t,x) \sim \mathcal{N}(x + \dot{x} \Delta t + \frac{1}{2} \ddot{x} \Delta t^2,\frac{1}{4}\Delta t^4 \sigma^2) $$

与后验无关，由上式可知，$x'$和$\dot{x}'$的后验概率分布与后继状态无关。

2. 再次考虑习题1中的动态机器人。为计算从机器人初始位置$x$和初始速度$\dot{x}$到最终位姿$x'$和最终速度$\dot{x}'$的后验分布提供一个数学公式。这个后验值得注意的是什么？

1. 每个仿真时间间隔中的加速度不是累加的，而是给定加速度和高斯噪声之和。也就是说，每个时间间隔的加速度之间是独立的。
2. 虽然加速度之间是独立的，但是因为后验表达式中没有后继状态，因此后继状态与后验仍然无关。

3. 假设控制的机器人在$T$时间间隔具有随机加速度，这里$T$值较大。最终的位置$x$和速度$\dot{x}$是相关的吗？如果是，它们随着$T\rightarrow\infty$是完全相关的吗，一个变量是另一个变量的确定函数吗？

由第一题的结论可知，在每个时间间隔$\Delta t$内，$x$与$\dot{x}$是正相关的。而随着$T$值的增大，从全局的角度来看，二者并不是完全相关，因为加速度是随机的。在每个$\Delta t$内，函数是确定的，但长期来看没有确定的函数。

4. 现在考虑一个理想自行车的简单运动学模型。两个轮胎直径为$d$，并被安装在长度为$l$的框架上。前轮胎绕一个垂直轴线转向，其转角用$\alpha$表示。后轮胎总是与自行车框架平行并且不能转向。本习题中，机器人的位姿用三个变量定义：相对于外部坐标系，前轮胎中心的$x-y$位置、自行车框架的角度方向$\theta$。控制是自行车的前向速度$v$和转向角$\alpha$，在每一个预测周期内假定其是恒定的。假定前向速度$v$和转向角$\alpha$均受到高斯噪声的影响，提供时间间隔$\Delta t$的数学预测模型。模型必须预测从一个已知状态开始$\Delta t$时间后的自行车状态的后验。如果不能找到一个精确的模型，近似它并解释这种近似。

问题的示意图如图所示：

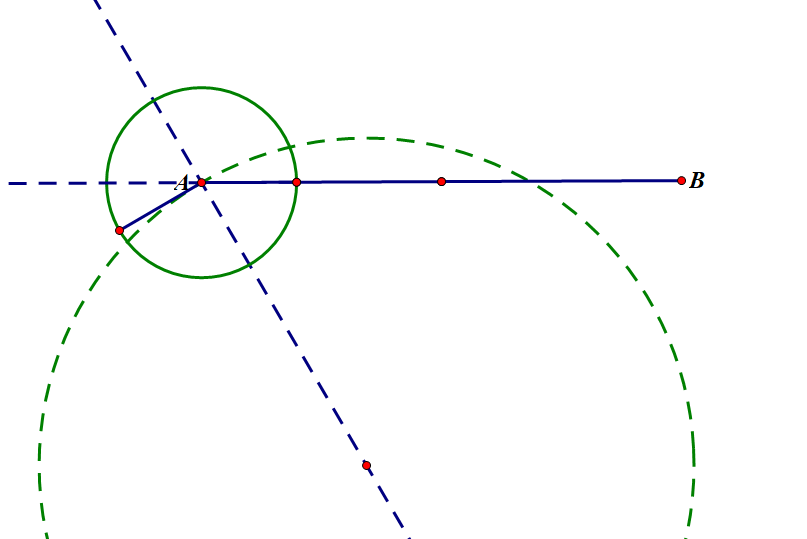
可以总结出关系如下：
前轮绕行一圈的周期为：$ T = \frac{2\pi}{\alpha} $
车身绕行的半径为：$ R = \frac{v}{\alpha}$
前轮绕行的半径为：$ r = \sqrt{\frac{l^2}{4}+R^2} $

这个$\frac{v}{cos(\alpha)}$可能难以理解。自行车的运动轨迹应该是一个圆形，前轮和后轮的轨迹应该是一个同心圆。根据普遍认知，自行车的前轮运动半径应该大于后轮。因此，前轮的运动速度认为是$\frac{v}{cos(\alpha)}$。

状态变量为$X = (x,y,\theta)^T$，其中，$x$、$y$为前轮中心二维直角坐标，$\theta$为自行车框架的角度。控制量为$u_t = (v,\alpha)$。

建立状态和控制之间的关系：
假设自行车车架中点的坐标为$(0,0)$，车架与y轴重合，$\theta$的初始值为0。车架应该绕$(-R,0)$，以$R$为半径的圆$O_1$运动。运行$\Delta t$时间后，车架中点的位置变为：
$$ (X,Y) = (Rcos(\alpha \Delta t)-R,sin(\alpha \Delta t)) $$
自行车前轮中心点的起始点为$(0,\frac{l}{2})$，自行车绕前轮中心应该绕$(-R,0)$，以$\sqrt{\frac{l^2}{4}+R^2}$为半径的圆$O_2$转动。那么自行车前轮中心的坐标应该为：
$$ (x,y) = (r \cdot cos(\alpha \Delta t + arctan(\frac{l}{2R})),r \cdot sin(\alpha \Delta t + arctan(\frac{l}{2R}))) $$

状态的表达式应该为：

$$ X_{t+1} = \begin{pmatrix}
x_{t+1} \\ y_{t+1} \\ \theta_{t+1}
\end{pmatrix} = \begin{pmatrix}
\sqrt{\frac{l^2}{4}+R^2} \cdot cos(\alpha \Delta t + arctan(\frac{l}{2R}))-R \\
\sqrt{\frac{l^2}{4}+R^2} \cdot sin(\alpha \Delta t + arctan(\frac{l}{2R}))\\
\alpha \Delta t
\end{pmatrix} $$

其中，$ess_v \sim \mathcal{N}(0,\sigma_1^2)$，$ess_\alpha \sim \mathcal{N}(0,\sigma_2^2)$。

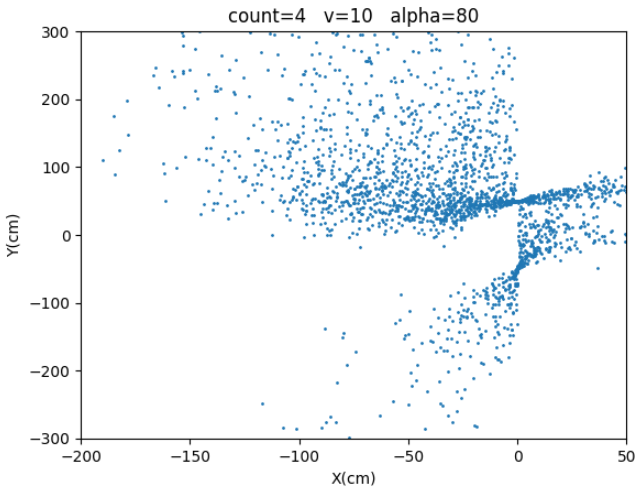
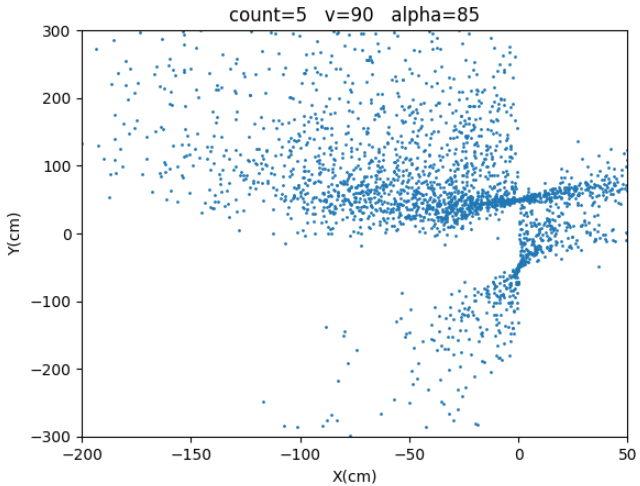
5. 考虑习题4的自行车运动学模型。在同样噪声假设下实现自行车后验位姿的采样函数。对于你的仿真，可以假定$l=100cm$，$d=80cm$，$\Delta t = 1s$，$|\alpha| \leq 80^o $ ，$v \in [0;100]cm/s$。进一步假定转向角的方差$\sigma_{\alpha}^{2} = {25^o}^2$，速度的方差为$\sigma_v^2 = (50cm^2/s^2)v^2$。注意速度的方差取决于给定的速度。对于原点开始的自行车，画出以下控制参数值产生的采样集。所有图都显示坐标轴和单位。

问题编号	$\alpha$	$v$
1	$25^o$	20cm/s
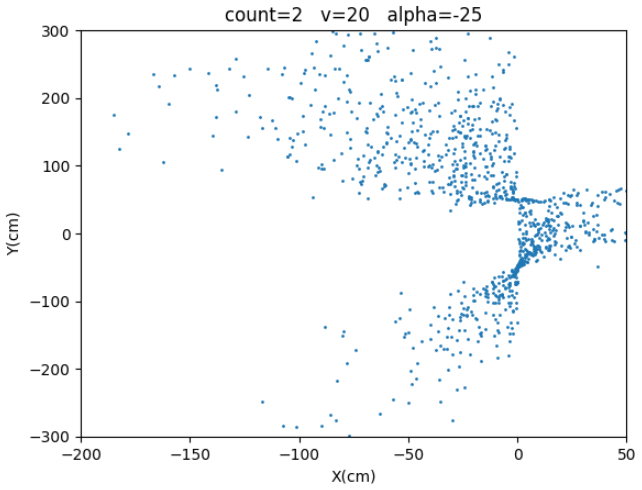
2	$-25^o$	20cm/s
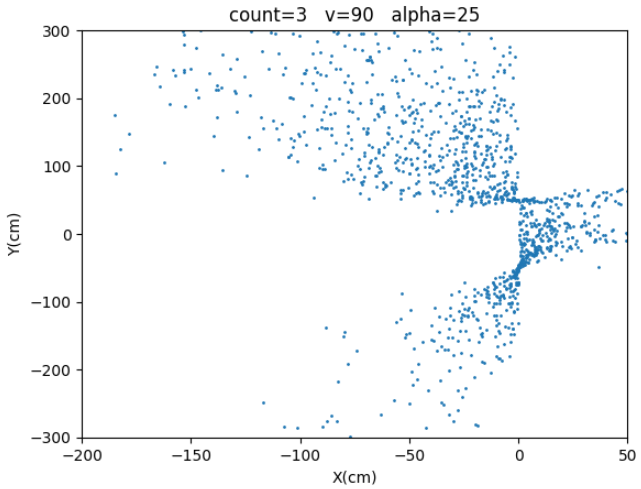
3	$25^o$	90cm/s
4	$80^o$	10cm/s
5	$85^o$	90cm/s

import matplotlib.pyplot as plt
import numpy as np
import random
import math

v = np.array([20,20,90,10,90])
alpha = np.array([25,-25,25,80,85])

x = np.empty(0)
y = np.empty(0)

for i in range(0,5):
    plt.title("count="+str(i+1)+"   v="+str(v[i])+"   alpha="+str(alpha[i]))
    plt.xlabel('X(cm)')
    plt.ylabel('Y(cm)')
    plt.xlim(-200,50)
    plt.ylim(-300,300)
    #计算速度标准差
    sigma_v = math.sqrt(50)*v[i]
    v_rand = np.random.normal(loc=v[i],scale=sigma_v,size=(1,1000)).flatten()
    alpha_rand = np.random.normal(loc=alpha[i],scale=25,size=(1,1000)).flatten()
    alpha_rand = np.dot(alpha_rand,math.pi/180)
    for cnt in range(0,1000):
        R = math.sqrt(2500 + v_rand[cnt]*v_rand[cnt]/alpha_rand[cnt]/alpha_rand[cnt])
        tmp = math.atan(50/R)
        x = np.append(x,R*math.cos(alpha_rand[cnt]+tmp)-v_rand[cnt]/alpha_rand[cnt])
        y = np.append(y,R*math.sin(alpha_rand[cnt]+tmp))
        theta = alpha_rand[cnt]
        #print(x,y)
    plt.scatter(x,y,s=1)
    plt.show()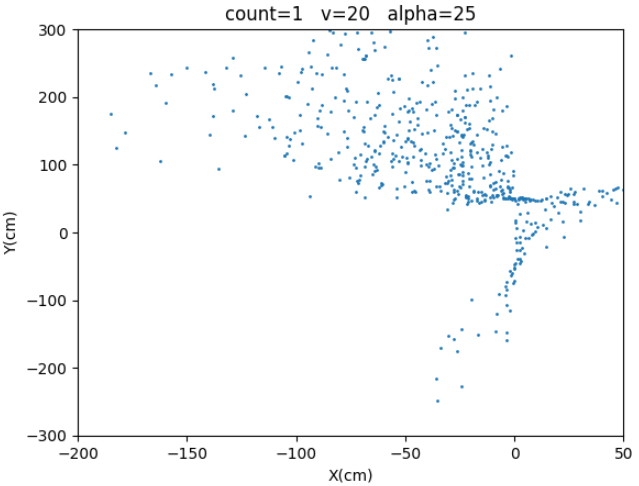

6. 再一次考虑习题4的自行车的运动学模型。给定初始状态$x、y、\theta$和最终的$x'$和$y'$（但没有最终的$\theta'$），提供一个确定最可能的$\alpha、v、\theta'$值的数学公式。如果你不能找到一个闭式解，请给出近似该值的一种技术。

系统输入：初始状态$(x,y,\theta)$、最终状态$(x',y')$。
系统输出：控制$(\alpha、v)$、最终状态$\theta'$。

由第4题：

$$ X_{t+1} = \begin{pmatrix}
x_{t+1} \\ y_{t+1} \\ \theta_{t+1}
\end{pmatrix} = \begin{pmatrix}
\sqrt{\frac{l^2}{4}+R^2} \cdot cos(\alpha \Delta t + arctan(\frac{l}{2R}))-R \\
\sqrt{\frac{l^2}{4}+R^2} \cdot sin(\alpha \Delta t + arctan(\frac{l}{2R}))\\
\alpha \Delta t
\end{pmatrix} $$

为了简化计算，假设$x=0,y=0,\theta=0$，可知：
$$ \begin{cases}
x' = \sqrt{\frac{l^2}{4}+R^2} \cdot cos(\Delta \theta + arctan(\frac{l}{2R}))-R \\
y' = \sqrt{\frac{l^2}{4}+R^2} \cdot sin(\Delta \theta + arctan(\frac{l}{2R})) \end{cases}$$

可以看出，可以找到闭式解。先求R：
$$ ({x'}+R)^2+{y'}^2=\frac{l^2}{4}+R^2 \\
{x'}^2 + {y'}^2 + 2Rx' = \frac{l^2}{4}\\
R = \frac{l^2}{8x'}-\frac{x'}{2}-\frac{{y'}^2}{2x'}$$

再求$\Delta \theta$：
$$ \Delta \theta = arcsin(\frac{y'}{\sqrt{\frac{l^2}{4}+R^2}})-arctan(\frac{l}{2R}) $$

已知$\Delta \theta$、$R$、$v$、$\alpha$之间存在关系：
$$ \Delta \theta = \theta' - \theta = \alpha \Delta t\\
R = \frac{v}{\alpha}$$

容易求得：
$$ v = R \times \frac{\Delta \theta}{\Delta t} \\ \alpha = \frac{\Delta \theta}{\Delta t} $$

7. 室内机器人的常用驱动器是完整的（holonomic）。一个完整的机器人具有与其配置（或姿态）的维数相同的可控自由度。在本习题中，请概括操作在平面上的完整机器人的速度模型，假定机器人能控制其前向速度，正交侧向速度和一个旋转角速度。规定向左侧向运动为正值，向右侧向运动为负值。

（1）陈述这样一个机器人的数学模型，假定其控制受到独立高斯噪声的影响。

（2）给出计算$p(x_t|u_t,x_{t-1})$的过程。

（3）给出采样$x_t \sim p(x_t|u_t,x_{t-1})$的过程。

（1）

位姿
$$ pose = \begin{pmatrix} x \\ y \\ \theta \end{pmatrix} $$

控制
$$ u = \begin{pmatrix} v \\ w \end{pmatrix} $$

（2）计算概率$p(x_t|u_t,x_{t-1})$的可能算法见如下程序：
$Algorithm~Motion\_Model\_Velocity(x_t,u_t,x_{t-1}):$
  $\mu = \frac{1}{2} \frac{(x-x')cos\theta + (y-y')sin\theta}{(y-y')cos\theta - (x-x')sin\theta} $
  $x^{*}=\frac{x+x'}{2} + \mu (y-y')$
  $y^{*}=\frac{y+y'}{2} + \mu (x-x')$
  $r^{*}=\sqrt{(x+x')^2 + (y+y')^2}$
  $\Delta\theta = atan2(y'-y^{*},x'-x^{*})-atan2(y-y^{*},x-x^{*})$
  $\hat{v} = \frac{\Delta\theta}{\Delta t} r^{*}$
  $\hat{w} = \frac{\Delta\theta}{\Delta t}$
  $\hat{\gamma} = \frac{\theta^{'}-\theta}{\Delta t}-\hat{w}$
  $return~prob(v-\hat{v},\alpha_1 v^2+\alpha_2 w^2) \cdot prob(w-\hat{w},\alpha_3 v^2+\alpha_4 w^2) \cdot prob(\hat{\gamma},\alpha_5 v^2,\alpha_6 w^2)$

（3）采样过程见如下程序：
$Algorithm~sample\_motion\_model\_velocity(u_t,x_{t-1}):$
  $\hat{v} = v + sample(\alpha_1 v^2 + \alpha_2 w^2)$
  $\hat{w} = w + sample(\alpha_3 v^2 + \alpha_4 w^2)$
  $\hat{\gamma} = sample(\alpha_5 v^2 + \alpha_6 w^2)$
  $x' = x - \frac{\hat{v}}{\hat{w}}sin \theta + \frac{\hat{v}}{\hat{w}}sin (\theta + \hat{w}\Delta t)$
  $y' = y + \frac{\hat{v}}{\hat{w}}sin \theta - \frac{\hat{v}}{\hat{w}}sin (\theta + \hat{w}\Delta t)$
  $\theta' = \theta + \hat{w}\Delta t + \hat{\gamma}\Delta t$
  $return~x_t = (x',y',\theta')^T$